Introduction

    This lab aims to conduct astrophysics computation for understanding the formation of large-scale structures where dark matter particles are the dominant constituent and the formation of galaxies where baryons play the crucial role.  This lab also explores an alternative dark matter model, where the extremely light dark matter is in the form of Bose-Einstein condensate.  In addition to the massively parallel computation, we also take advantage of the simulation data and conduct researches on gravitational lensing, Sunyaev-Zeldovich effects of microwave background radiation, galaxy groups and clusters identifications, etc.

    As far as the computation technology, it is our strategy that our lab is willing to modify computers and experiment any available advanced technology for building a low-cost niche supercomputer.  With innovations, we intend to compete against other groups that have access to Top-500 supercomputers. For example, we were among the leading groups in 2007 that adopt graphic cards as the main computational engine in our 16-node PC cluster, GraCCA (Fig(1)).  We began this supercomputer project in 2006 when the general computational usage of Graphic Processor Unit (GPU) was obscure and it was necessary to program pixel engines and vertex engines in terms of 2D graphic processing for 3D physics computation.  During this period, we conducted the 3D Belousov-Zhabotinsky reaction computation for demonstration of the power of GPU. Partial results are given in Fig.(2).

                                

Fig.(1): In the 16-node GraCCA, each node is equipped with two graphic cards.

Fig.(2): 3D Belousov-Zhabotinsky reaction at different times and in different perspectives, where a 3D intrusion grows out of two active slices at different Z.

    In the past few years after adopting the GPU computation, we commonly experienced a “memory space” problem.  Due to the limited memory space in a PC cluster, it is impossible to conduct computations for problems requiring several terabytes memory space.  Despite the computational speed of a GPU cluster can be comparable to that of a Top-500 supercomputer, the problem size is far smaller.  This finding comes with no surprise because what makes a Top-500 supercomputer expensive is its large available memory space.  The goal of our technical team in the next years is to identify a solution to this memory-space problem for the GPU cluster. 

    Our strategy is to design and make a proprietary card that allows 16 hard disks to be connected to one PC, where each hard disk can execute IO at its full speed.  When so, we can use the storage devices as the pseudo-memory of the GPU cluster and solve the memory space problem.   We find that the very same technique can have wide commercial applications in machines that require extremely high IO bandwidth, such as 3D-movie player, 3D medical imager, etc.

(a) Gravitational Lensing

Gravitational lensing is produced by intervening massive bound objects in between the light source and the observer, and distorts the space time.  In the time domain the distortion results in different travel times for two rays coming from the same source.  In the space domain, the distortion creates more spectacular effects.

We can study these effects with our simulation data.  If a 2D uniform sheet is propagated backward in time along the local geodesic trajectories, at redshift z=1000, the sheet can be highly distorted.  The distortion along line-of-sight gives the time-domain distortion.  The distortion across the sky contains complex local stretch, shear and compression (Fig.(3)).  The 2D lensing map is the inverse of this 2D distortion map; for example, a highly compressed region in the latter will yield high magnification in the former.  A number of interesting science questions can be asked with the lensing map.  For example, what is the mass of the intervening bound object  to produce a certain lensing map, how well can the gravitational lensing act as a telescope to probe the z>2 galaxies?    

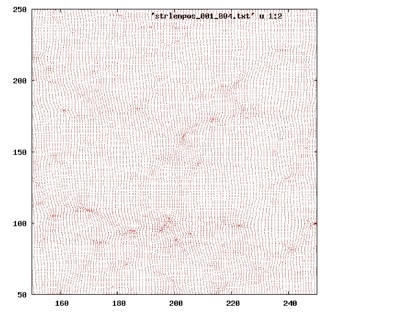
Fig.(3): A 2D distortion map when propagating a uniform mesh backward in time to z=1000.  This map is the inverse of the observed lensing map.

2. (b)Sunyaev-Zeldovich Effect (SZE):
   

When the cold CMB photons pass through a potential well containing hot baryons, these photons can gain energy through inverse Compton scattering.  The net result to these encountered photons is the deviation from the original black-body spectrum.  This effect is called SZE.  It is the secondary CMB anisotropy generated in late epochs of cosmic evolution.  It is a small effect but can be measurable when using a specially designed telescope, such as NTU-Array and others.  The SZE allows us to probe very distant bound objects.  This is because the light source is CMB which comes from redshift z=1100, and any object in between z=1100 and z=0 can produce SZE of comparable strength.  This powerful effect provides perhaps the only tool to systematically search for bound objects beyond z=5 if any was to exist then.  Our simulation data can be used to produce the CMB sky including SZE (Fig.(4)), with which one may ask how realistic such a z>5 bound object survey is when the foreground contamination is taken into account. 

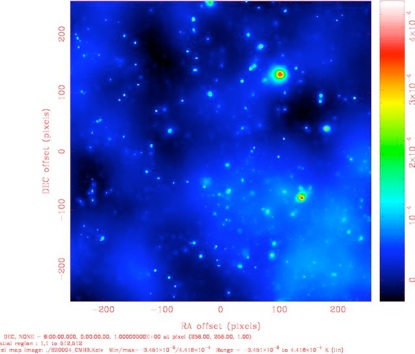
Fig.(4): One squared degree of CMB sky including SZE, where the brighter spots and dots are produced by SZE.  On the other hand, the cloud-like diffuse pattern is the CMB primary anisotropy.

100. (c)Identification of Galaxy Groups
     

Galaxies are rarely existent in isolation, and galaxy groups are the most common structures in the universe.  However, galaxy groups are difficult to identify simply because their members do not necessarily have similar colors.  This aspect is in great contrast to galaxy clusters, where their members are mostly red.  With an semi-empirical galaxy identification model, we may attempt to identify galaxy groups and clusters with the simulation data.  Since the galaxy redshifts cannot be determined to a high degree of accuracy with the photometric method, the identified group has some degrees of uncertainty.  Simulation data allows us to estimate how accurate one may hope to identify galaxy groups optically.  Shown in Fig.(5) is a 2D map of galaxy distribution in a common halo, where galaxies are marked in green and dark matter particles are marked in red.  We note that the group members do not necessarily interact with each other directly through gravity; however they are bound together by a common deep gravitational potential.  It is only for those close pairs that interact with each other directly, and these pairs are on the verge of merging, which is responsible for galaxy mass growth.

Fig.(5): A halo of tens of galaxies of various sizes.

500. (d)High IO bandwidth GPU Cluster: 
     

A prototype has been built to test the IO bandwidth while running a realistic hydrodynamic GPU code (Fig.(6)).  Using the commodity devices, eight hard disks are connected to a single GPU mother board.  The theoretical peak IO bandwidth amounts to 1000MB/s for read or write.  With special designs for the GPU hydrodynamic code, we demonstrate that the IO bandwidth can reach 950MB/s for read operations and 700MB/s for write operations when using the 8 hard disks as the pseudo-memory in the run (Fig.(7)).  With proper error-correction algorithm to reduce the number of IO, the IO time can be made a factor of few shorter than the computation time.  This optimized throughput performance gives us confidence that a low-cost genuine supercomputer can be built with this scheme. When equipped with the proprietary card, the IO bandwidth can be enhanced by a factor of 2 compared with the prototype so that one may cope with the twice faster new-generation GPU. 

Fig.(6): A single-node prototype GPU supercomputer that is connected to 8 hard disks as its pseudo-memory.  

Fig.(7) IO bandwidth of the prototype after optimization.  The GPU computing time is still longer than the IO time by a factor of few.

5. (e)Dark Matter in BEC State
   

If the dark matter particle mass is extremely small, the temperature under which BEC occurs can be very high, rendering all dark matter particles in the BEC ground state.  In this case, all particles evolve coherently and are described by a single wave function, satisfying the Schroedinger-Poisson’s equation.  Cosmic structure formation can still proceed above the galaxy scale as the conventional cold dark matter does, but small scale structures are severely suppressed by the uncertainty principle.

We may simulate this Schroedinger-Poisson system starting from a random initial condition.  Shown in Fig.(8) is the detailed structure of a gravitationally collapsed object that is located at the junction of two filaments.

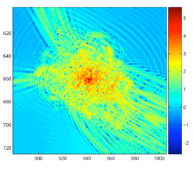
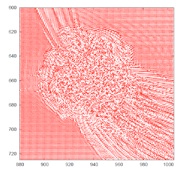
Fig.(8): Density (left) and normalized velocity (right) of a gravitationally collapsed object.  Note from the velocity plot that there is a well defined boundary, marking approximately the virial radius.  The bound object is located at the junction of two filaments, with can be clearly seen in the velocity plot.  

6. (f)Quantum Turbulence
   

Cosmic structure formation is a manifestation of turbulence in a collisionless medium.  BEC turbulence on the other hand has been claimed to resemble turbulence of ordinary fluid.  However, the result of BEC turbulence is mostly derived from numerical simulations, which can suffer from various numerical errors on small scales.

To resolve this problem, we construct a soluble quantum turbulence model, where cascade of turbulence energy is observed over a finite time interval.  When the cascade stops, the system is in a statistically stationary state, exhibiting a power law energy spectrum.  We identify such an energy spectrum to be due to the appearance of entangled quantum vortex lines that are created and annihilated without the need of dissipation (Figs.(9) and (10)).

Fig.(9): Steady-state 3D quantum turbulence comprising a number of moving vortex lines.

Fig.(10):  Detailed structure of a sheet of vortex filaments near the onset of vortex creation.

7. (g)Adaptive-Mesh-Refinement Code
   

In Astrophysics, gravity plays the central role.  However, a gravitational system tends to have negative energy, rendering the system unstable to formation of ever denser bound objects.  Therefore, astrophysics simulations must cope with this unstable situation and to resolve the internal structure of a dense object.

Fortunately, mass is conserved during the gravitational contraction, and hence  dense regions are highly localized in small volumes.  That is, only high-density regions of small volume require high resolution.  We can take advantage of this property to simplify the problem.  The Adaptive-Mesh-Refinement code is specifically tailored to handle this kind of problem.  The computational meshes automatically become finer in real time when the code detects higher density.  Figure (11) shows an example of how the code copes with a gravitationally collapsed object in a cosmological simulation.

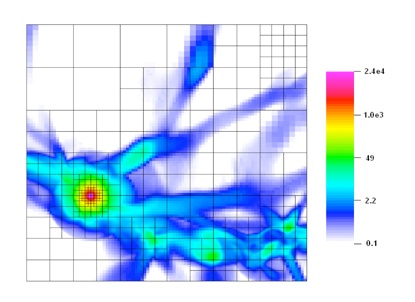
Fig.(11) Refined meshes created around a gravitationally collapsed object in a cosmological simulation, where the color indicates the density.

We have recently built a GPU-accelerated Adaptive-Mesh-Refinement code and begun to conduct cosmological simulations.  The use of GPU can shorten the run time by an impressive factor of 12.  The following link is a presentation file of this code.

1. Gamer: GPU-accelerated Adaptive-MEsh-Refinement & Out-of-core Computation [PDF]

2. 2.Gamer: A Graphic Processing Unit Accelerated adaptive-Mesh-Refinement Code for Astrophysics [PDF]
   

3. 3.Graphic-card cluster for astrophysics (GraCCA) – Performance tests [PDF]
   

Back...

Researches