Quantum Information and Manybody Physics

Quantum information science is an emerging frontier that has generated a great deal of interests and stimulated novel potential applications. Its aim is to understand how certain fundamental laws of quantum physics can be harnessed to dramatically improve the storage, processing and transmission of information. On the other hand, quantum manybody systems give rise to exotic collective states of matter, such as superfluids, superconductors, and insulating quantum liquids, which have no classical counterparts. Significant progress has been made in our understanding toward the collective behavior of quantum manybody systems via both analytical and numerical approaches.

Analytical approaches can often provide qualitative guidance. Unbiased numerical simulations play a crucial role in verifying the underlying assumptions. However, there are important classes of problems, such as fermionic systems, frustrated spin systems, and non-equilibrium quantum systems, which are still impossible to obtain solutions via direct simulation.

In recent years, interplay between concepts from quantum information theory, and novel numerical methods have improved our understanding of the reason behind the difficulties of these classes of problems, and various new ideas from the quantum information theory provide potential breakthroughs to overcome these challenges.

The matrix product state (MPS) representation is the key ingredient behind the success of the density-matrix renormalization group algorithm, and leads to a

n efficient representation of the ground state when the amount of entanglement in the system is sufficiently small. For its higher dimensional extension, the tensor product states(TPS), we constructed a method for contracting the tensor network in two dimensions, based on auxiliary tensors accomplishing successive truncations (renormalization) of 8-index tensors for 2×2 plaquettes into 4-index tensors. The scheme is variational, and thus the tensors can be optimized by minimizing the energy. Test results for the quantum phase transition of the transverse-field Ising model confirm that even the smallest possible tensors (two values for each tensor index at each renormalization level) produce much better results than the simple product (mean-field) state.

Furthor information

1. •L. Wang, YJK, A.W. Sandvik, Plaquette Renormalization Scheme for Tensor Network States, arXiv:0901.0214
   

2. •Chen Liu, Ling Wang, Anders W. Sandvik, Yu-Cheng Su, Ying-Jer Kao, Symmetry breaking and criticality in tensor-product states, arXiv:1002.1657

Geometrical Frustrated Magnets

Magnetic spin systems with geometrical frustration exhibit very rich physics. The large number of ground state degeneracy due to geometrical frustration introduces extra difficulties to systematically study these problems theoretically.

Spin ice materials have received great attention in the past decade due to their fascinating properties and complex behaviors. These materials are magnets with ferromagnetic interactions on the geometrical frustrated pyrochlore lattice with strong single-ion anisotropy. The presence of local, non-collinear easy axes in these materials leads to pseudo Ising spins with effective antiferromagnetic interactions, and the system is strongly frustrated. The magnetic moments thus obey the same ice rules as water ice at low temperatures, with two spins pointing into the center of each tetrahedron and two spins out. This local 2-in-2-out constraint gives rise to a large degrees of ground state degeneracy, which results in nonzero entropy density at absolute zero temperature. Recently, excitations above the degenerate ground state manifold, i.e., defects in the spin ice state, are proposed to be well described as magnetic monopoles of opposite “charge” in the background of “Dirac strings”. Finite energy is required to separate these monopoles to infinity, i.e., they are deconfined, and they interact via the magnetic Coulomb interaction. On the other hand, when a magnetic field is applied along the [100] direction, the spin ice would approach saturated magnetization through a topological 3D Kasteleyn transition at low temperature, and the low energy magnetic excitation involves a collection of spins on a string spanning the system.

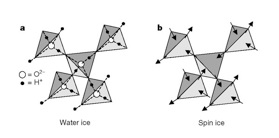
Furthor information

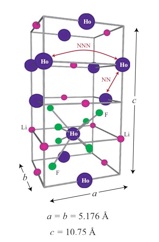
1. •Y. Z. Chou, YJK, Quantum Order by Disorder in a Semi-classical Spin Ice, arXiv:1005.4742
   

2. •L. J. Chang, Y. Su, Y. -J. Kao, Y. Z. Chou, R. Mittal, H. Schneider, Th. Brueckel, G. Balakrishan, M. R. Lees, Magnetic correlations in spin ice Ho2-xYxTi2O7 as revealed by neutron polarization analysis, arXiv:1003.4616

Simulation of exotic phases and phase transitions in quantum lattice models

In 2004, Kim and Chan reported signatures of superfluidity in solid 4He in torsional oscillator experiments,where a drop in the resonant period, observed at around T ~0.2 K, suggested the existence of a nonclassical rotational inertia in the crystal. Following the discovery by Kim and Chan, many experiments and theories have attempted to explain this fascinating observation; the situation remains, however, controversial.

We use Gutzwiller mean field theory and Stochastic Series Expansion (SSE) quantum Monte Carlo (QMC) simulations to study the ground state phase diagram of the hard-core extended boson Hubbard

model on the square lattice with both nearest-  and next-nearest-neighbor hopping and repulsion. We observe the formation of supersolid states with checkerboard, striped, and quarter-filled crystal structures, when the system is doped away from commensurate fillings. In the striped supersolid phase, a strong anisotropy in the superfluid density is obtained from the simulations; however, the transverse component remains finite, indicating a true two-dimensional superflow. We find that upon doping, the striped supersolid transitions directly into the supersolid with quarter-filled crystal structure, via a first-order stripe melti

ng transition.

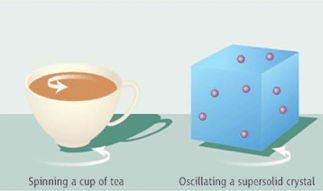
Further information:

1. •Yu-Chun Chen, Roger G. Melko, Stefan Wessel, Ying-Jer Kao, Supersolidity from defect-condensation in the extended boson Hubbard model, Phys. Rev. B 77, 014524 (2008)

Development of Efficient Algorithm

We developed a new algorithmic framework for a variant of the quantum Monte Carlo loop algorithm, in which non-local loop or cluster constructs in the d+1 dimensional simulation cell close in a way which makes each individual loop smaller. The algorithm is designed to increase simulation efficiency in cases where conventional loops become very large, or do not

close altogether – a situation which sometimes occurs in Hamiltonians with frustrating or competing interactions, on large lattices at low temperatures. We demonstrated and characterized some aspects of the short-loop on a simple 2-d XXZ model. This quantum short-loop algorithm will likely be most useful in complicated models (e.g. with long-range interactions in the Hamiltonian) where conventional long-loops are obs

erved to behave poorly - becoming excessively long or failing to close alltogether. We are currently extending it to models where conventional loop algorithms fail.

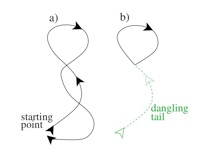
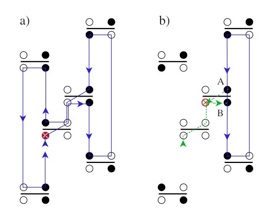
Further information

1. •Ying-Jer Kao, Roger G. Melko, A short-loop algorithm for quantum Monte Carlo simulations, Phys. Rev. E 77, 036708 (2008)
   

Disordered Systems

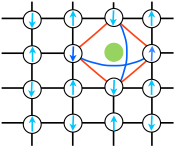
Impurities are known to be an effective tool to locally perturb quantum systems, thereby revealing important information about their microscopic interactions and correlations.

The LiHoxY1-xF4 magnetic material in a transverse magnetic field perpendicular to the Ising spin direction has long been used to study tunable quantum phase transitions in a random disordered system. We show that the transverse-field-induced magnetization, combined with the local random dilution-induced destruction of crystalline symmetri

es, generates, via the predominant dipolar interactions between Holmium ions, random fields along the Ising direction. This identifies LiHoxY1-xF4 in a transverse field as a new random field Ising system. The random fields explain the rapid decrease of the critical temperature in the diluted ferromagnetic regime and the smearing of the nonlinear susceptibility at the spin-glass transition with increasing the transverse field. This is an important discovery since this material can be studied easily and with high precision with current technologies. This will advance our understandings of the random field problem, and may also suggest a mechanism for tuning the strength of domain wall pinning, which is important for applications.

Using the exam

ple of Zn-doped La2CuO4 , we demonstrate that a spinless impurity doped into a nonfrustrated antiferromagnet can induce substantial frustrating interactions among the spins surrounding it. This result is the key to resolving discrepancies between experimental data and earlier theories. Analytic and quantum Monte Carlo studies of the impurity-induced frustration are in a close accord with each other and experiments. The proposed mechanism should be common to other correlated oxides.

Further information

1. •S.M.A. Tabei, M.J.P. Gingras, Y.-J. Kao, P. Stasiak, J.-Y. Fortin ,Induced Random Fields in the LiHoxY1-xF4 Quantum Ising Magnet in a Transverse Magnetic Field, Phys. Rev. Lett. 97, 237203 (2006)
   

2. •S.M.A Tabei, M.J.P. Gingras, Y.-J. Kao, T. Yavors'kii, Perturbative Quantum Monte Carlo Study of LiHoF4 in a Transverse Magnetic Field, Phys. Rev. B 78, 184408 (2008)
   

3. •Cheng-Wei Liu, Shiu Liu, Ying-Jer Kao, A. L. Chernyshev, Anders W. Sandvik , Impurity-induced frustration in correlated oxides, Phys. Rev. Lett. 102, 167201 (2009)

High Performance Computing Using GPU

As the programmability and performance of modern graphics  processing units(GPUs) continues to increase, many researchers are looking to graphics hardware to solve problems previously performed on general purpose CPUs. In many cases, performing general purpose computation on graphics hardware can provide a significant advantage over implementations on traditional CPUs. In the past few years, t

he programmable graphics processor unit has become a computing workhorse.The specialized hardware in floating point computation gives GPU the edge to outperform traditional CPUs. Large-scale parallel computing has until recently remained the realm of large server clusters and supercomputers. GPU has great potential for solving  problems that can be divided into many smaller elements and analyzed in parallel. GPU computing makes supercomputing possible with any PC or workstation and expands the power of server clusters to solve problems that were previously not possible with existing

CPU clusters. GPU computing is a new front for scientific computation. We are designing programs for simulations in strongly correlated systems.