Ruey-Lin Chern
Professor
Institute of Applied Mechanics
National Taiwan University
Tel: 886-2-3366-5853
Fax: 886-2-2363-9290
Email: chernrl at ntu.edu.tw
Address: No.1, Sec. 4, Roosevelt Rd., Taipei 106, Taiwan

Use Google Chrome browser for better performance and appearance. Submit any suggestions to chernrl at ntu.edu.tw.
Curriculum vitae 

Ruey-Lin Chern received his Ph.D. degree in Applied Mechanics from National Taiwan University in 1991. He was an Assistant Researcher in Chung-Shan Institute of Science and Technology from 1992 to 2002. From 2002 to 2004 he was a Postdoctoral Fellow in Institute of Physics, Academia Sinica. In 2004, he joined National Taiwan University as an Assistant Professor in Institute of Applied Mechanics, and became Professor in 2011. In 2006, he received the best paper contribution award from the Center of Nanostorage Research at National Taiwan University. In the summer of 2007, he was a Visiting Associate in Department of Mechanical Engineering, California Institute of Technology. In 2009 and 2014, he received the excellent teaching award at National Taiwan University. His current research interests are in the area of nanophotonics, which includes photonic crystals, plasmonic structures, and electromagnetic metamaterials as major research topics.
Education
Ph.D. degree, Institute of Applied Mechanics, National Taiwan University, 1991
Master degree, Institute of Applied Mechanics, National Taiwan University, 1988
Bachelor degree, Department of Naval Architecture, National Taiwan University, 1986
Experience
Professor, Institute of Applied Mechanics, National Taiwan University, 2011~Present
Associate Professor, Institute of Applied Mechanics, National Taiwan University, 2007~2011
Visiting Associate, Department of Mechanical Engineering, California Institute of Technology, 2007.7~2007.9
Assistant Professor, Institute of Applied Mechanics, National Taiwan University, 2004~2007
Postdoctoral Research Fellow, Institute of Physics, Academia Sinica, 2002~2004
Assistant Researcher, First Institute, Chung-Shan Institute of Science and Technology, 1992~2002
Research 
Our current research field is nanophotonics, which includes photonic crystals, plasmonic structures, and electromagnetic metamaterials as three major research topics. We are devoted to studying the physical mechanisms behind important phenomena in these topics and to designing or improving the structures or materials with more or better functions based on these mechanisms. Our approaches to the problem are analytical derivations and numerical simulations by coding or running packages. Experimental cooperations with other groups in NTU and Academia Sinica are on the way.
Photonic Crystals
Photonic crystals are periodic structures made of dielectrics, metals, or other materials, with the lattice constant comparable with the wavelength of electromagnetic wave. One of the most distinguished features is the photonic band gap, a forbidden frequency range for waves to propagate in the crystal.
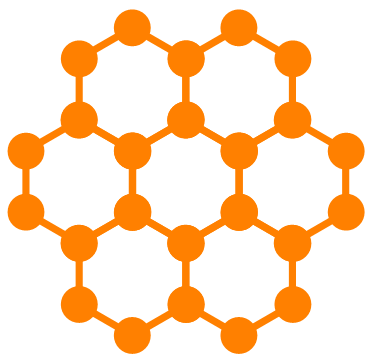
The following diagram is the photonic crystal composed of connected hexagonal lattice, which exhibits a large full band gap.
[1] R. L. Chern, C. C. Chang, C. C. Chang, and R. R. Hwang, "Large full band gaps for photonic crystals in two dimensions computed by an inverse method with multigrid acceleration", Physical Review E 68, 026704 (2003) [LINK]
[2] R. L. Chern, C. C. Chang, C. C. Chang, and R. R. Hwang, "Numerical Study of Three-Dimensional Photonic Crystals with Large Band Gaps", Journal of the Physical Society of Japan 73, 727 (2004) [LINK]
[3] R. L. Chern, C. C. Chang, C. C. Chang, and R. R. Hwang, "Two Classes of Photonic Crystals with Simultaneous Band Gaps", Japanese Journal of Applied Physics 43, 3484 (2004) [LINK]
[4] C. C. Chang, J. Y. Chi, R. L. Chern, C. C. Chang, C. H. Lin, and C. O. Chang, "Effect of the inclusion of small metallic components in a two-dimensional dielectric photonic crystal with large full band gap", Physical Review B 70, 075108 (2004) [LINK]
[5] H. K. Fu, Y. F. Chen, R. L. Chern>, and C. C. Chang, "Connected hexagonal photonic crystals with largest full band gap", Optics Express 13, 7854 (2005) [LINK]
[6] R. L. Chern and S. D. Chao, "Optimal higher-lying band gaps for photonic crystals with large dielectric contrast", Optics Express 16, 16600 (2008) [LINK]
[7] R. L. Chern, D. Felbacq, "Artificial magnetism and anticrossing interaction in photonic crystals and split-ring structures", Physical Review B 79, 075118 (2009) [LINK]
[8] R. L. Chern and Y. C. Lan, "Collective modes in metallic photonic crystals with subwavelength grooves", Physical Review B 80, 033107 (2009) [LINK]
[9] R. L. Chern and Y. T. Chen, "Effective parameters for photonic crystals with large dielectric contrast", Physical Review B 80, 075118 (2009) [LINK]
[10] R. L. Chern, D. Felbacq, "Resonant cavitylike modes in dielectric photonic crystals made of collections of subwavelength cylinders", Physical Review B 80, 205115 (2009) [LINK]
Plasmonic Structures
Plasmonic structures are conductors that support collective excitation of electrons, coupled with the external electromagnetic waves. Surface plasmon resonance is one of the most important features in these structures, which provides practical applications such as waveguides and sensors.
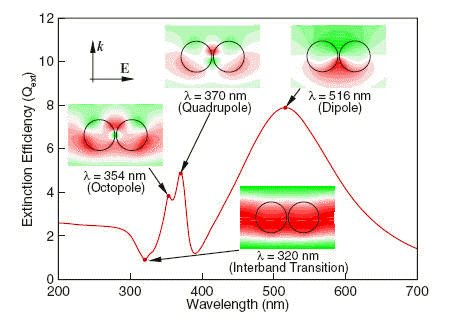
The following figure is a plot of the extinction efficiency for a pair of silver nanoparticles, showing the plasmonic resonances associated with dipole, quadrupole, and octopole modes.
[1] C. C. Chang, R. L. Chern, C. C. Chang, and R. R. Hwang, "Interfacial operator approach to computing modes of surface plasmon polariton for periodic structures", Physical Review B 72, 205112 (2005) [LINK]
[2] R. L. Chern, C. C. Chang, and C. C. Chang, "Analysis of surface plasmon modes and band structures for plasmonic crystals in one and two dimensions", Physical Review E 73, 036605 (2006) [LINK]
[3] R. L. Chern, C. C. Chang, and C. C. Chang, "Interfacial operator approach to computing band structures for photonic crystals of polar materials", Physical Review B 73, 235123 (2006) [LINK]
[4] R. L. Chern, X. X. Liu, and C. C. Chang, "Particle plasmons of metal nanospheres: Application of multiple scattering approach", Physical Review E 76, 016609 (2007) [LINK]
[5] R. L. Chern, "Surface plasmon modes for periodic lattices of plasmonic hole waveguides", Physical Review B 77, 045409 (2008) [LINK]
[6] R. L. Chern, "Interface matching method for solving surface plasmon modes with damping in plasmonic crystals", Physical Review E 79, 017701 (2009) [LINK]
[7] X. X. Liu, C. F. Tsai, R. L. Chern, D. P. Tsai, "Dispersion mechanism of surface magnetoplasmons in periodic layered structures", Applied Optics 48, 3102 (2009) [LINK]
[8] Y. T. Chen, R. L. Chern, and H. Y. Lin, "Multiple Fano resonances in metallic arrays of asymmetric dual stripes", Applied Optics 49, 2819 (2010) [LINK]
[9] R. L. Chern and W. T. Hong, "Transmission resonances and antiresonances in metallic arrays of compound subwavelength holes", Journal of Optics 12, 065101 (2010) [LINK]
[10] S. C. Lo, C. W. Yeh, S. H. Wang, C. W. Kuo, K. L. Lee, R. L. Chern, and P. K. Wei, "Self-referencing biosensors using Fano resonance in periodic aluminium nanostructures," Nanoscale 13, 17775 (2021) [LINK]
Electromagnetic Metamaterials
Metamaterials are artificial structures having unusual physical properties that are not available in naturally occurring materials, such as negative permeability or negative index of refraction. These unusual properties may come from the strong interaction of waves with the internal elements that compose the structure.
The following demo is an example of our research work, showing a Gaussian beam incident from vacuum onto a chiral medium for illustrating negative refraction and backward wave.
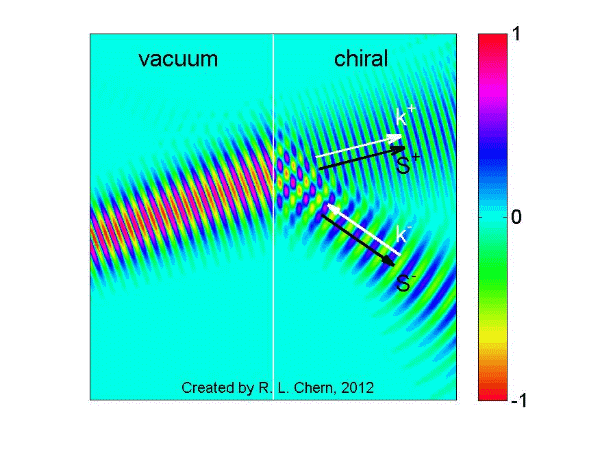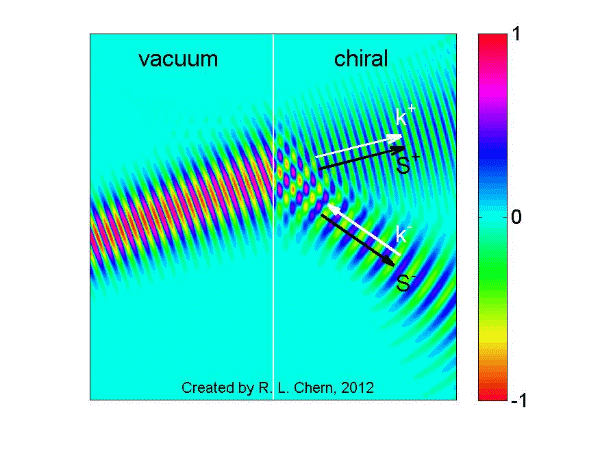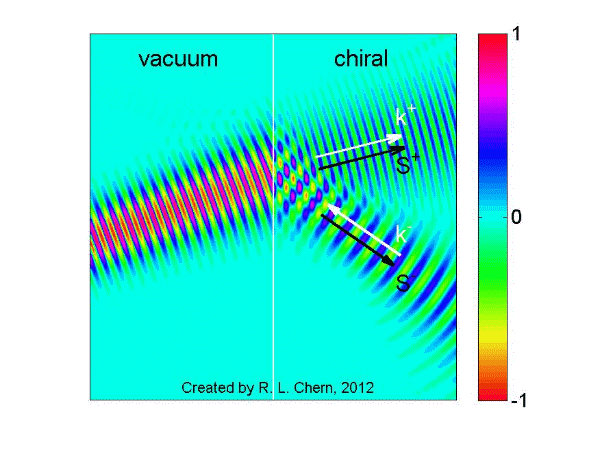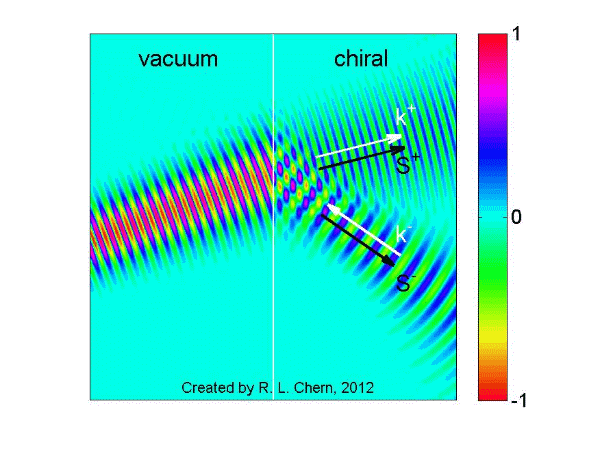
[1] R. L. Chern, C. C. Chang, and C. C. Chang, "Surface and bulk modes for periodic structures of negative index materials", Physical Review B 74, 155101 (2006) [LINK]
[2] Y. C. Lan and R. L. Chern, "Surface plasmon-like modes on structured perfectly conducting surfaces", Optics Express 14, 11339 (2006) [LINK]
[3] R. L. Chern, "Magnetic and surface plasmon resonances for periodic lattices of plasmonic split-ring resonators", Physical Review B 78, 085116 (2008) [LINK]
[4] R. L. Chern, "Large magnetic resonance band gaps for split ring structures with high internal fractions", Optics Express 16, 20186 (2008) [LINK]
[5] R. L. Chern and X. X. Liu, "Effective parameters and quasi-static resonances for periodic arrays of dielectric spheres", Journal of the Optical Society of America B 27, 488 (2010) [LINK]
[6] R. L. Chern, Y. T. Chen, and H. Y. Lin, "Anomalous optical absorption in metallic gratings with subwavelength slits", Optics Express 18, 19510 (2010) [LINK]
[7] C. H. Lin, R. L. Chern, and H. Y. Lin, "Polarization-independent broad-band nearly perfect absorbers in the visible regime", Optics Express 19, 415 (2011) [LINK]
[8] R. L. Chern and W. T. Hong, "Nearly perfect absorption in intrinsically low-loss grating structures", Optics Express 19, 8962 (2011) [LINK]
[9] R. L. Chern and P. H. Chang, "Negative refraction and backward wave in pseudochiral mediums: illustrations of Gaussian beams", Optics Express 21, 2657 (2013) [LINK]
[10] R. L. Chern and P. H. Chang, "Wave propagation in pseudochiral media: generalized Fresnel equations", Journal of the Optical Society of America B 30, 552 (2013) [LINK]
[11] R. L. Chern, "Anomalous dispersion in pseudochiral media: negative refraction and backward wave", Journal of Physics D: Applied Physics 46, 125307 (2013) [LINK]
[12] R. L. Chern and P. H. Chang, "Negative refraction and backward wave in chiral mediums: Illustrations of Gaussian beams", Journal of Applied Physics 113, 153504 (2013) [LINK]
[13] R. L. Chern, "Wave propagation in chiral media: composite Fresnel equations", Journal of Optics 15, 075702 (2013) [LINK]
[14] R. L. Chern, "Spatial dispersion and nonlocal effective permittivity for periodic layered metamaterials", Optics Express 21, 16514 (2013) [LINK]
[15] R. L. Chern and D. Han, "Nonlocal optical properties in periodic lattice of graphene layers", Optics Express 22, 4817 (2014) [LINK]
[16] R. L. Chern, "Effect of damping on Goos-Hanchen shift from weakly absorbing anisotropic metamaterials", Journal of the Optical Society of America B 31, 1174 (2014) [LINK]
[17] P. H. Chang, C. Y. Kuo, and R. L. Chern, "Wave propagation in bianisotropic metamaterials: angular selective transmission", Optics Express 22, 25710 (2014) [LINK]
[18] R. L. Chern, D. Han, Z. Q. Zhang, and C. T. Chan, "Additional waves in the graphene layered medium", Optics Express 22, 31677 (2014) [LINK]
[19] P. H. Chang, C. Y. Kuo, and R. L. Chern, "Wave splitting and double-slit like interference by a pseudochiral metamaterial slab", Journal of Physics D: Applied Physics 48, 295103 (2015) [LINK]
[20] R. L. Chern, M. C. Tsai, and Y. Z. Yu, "Cylindrical plasmonic waveguides with cladding of hyperbolic metamaterials", Journal of Lightwave Technology 35, 1995 (2017) [LINK]
[21] S. C. Lo, C. W. Lee, R. L. Chern, and P. K. Wei, "Hybrid modes in gold nanoslit arrays on Bragg nanostructures and their application for sensitive biosensors", Optics Express, 30, 30494 (2022) [LINK]
[22] S. C. Lo, S. H. Wang, T. W. Chang, K. L. Lee, R. L. Chern*, and P. K. Wei "Dual gold-nanoslit electrodes for ultrasensitive detection of antigen-antibody reactions in electrochemical surface plasmon resonance" ACS Sensors 7, 2597 (2022) [LINK]
Topological Photonics
Topological insulators are insulating in the bulk but possess conducting states on their surfaces. A remarkable feature of the topological phase is the emergence of gapless edge states that are protected by topology. The novel concepts of topological phases have also been extended to photonic systems, leading to the discovery of photonic topological insulators.
The following demo is an example of our research work, showing the propagation of a topologically protected surface wave on the hyperbolic-gyromagnetic metamaterial.
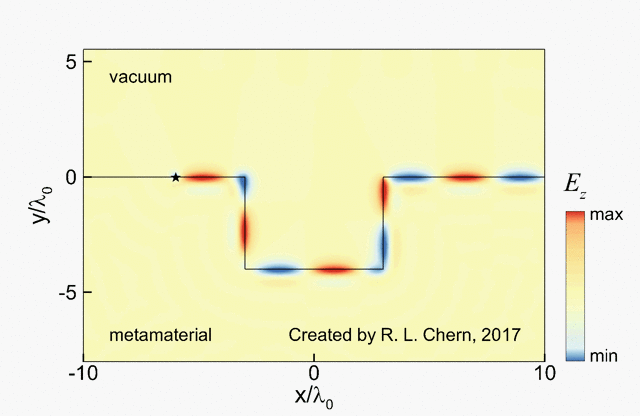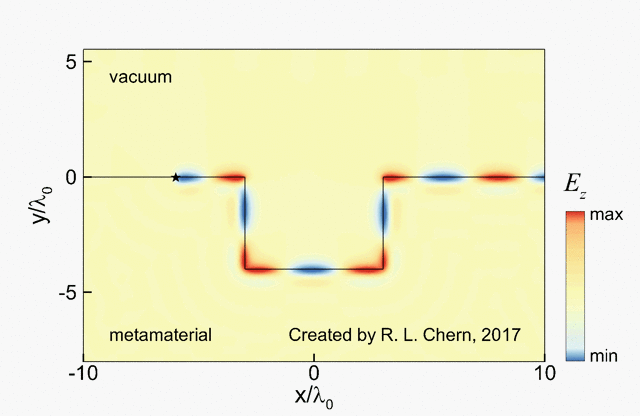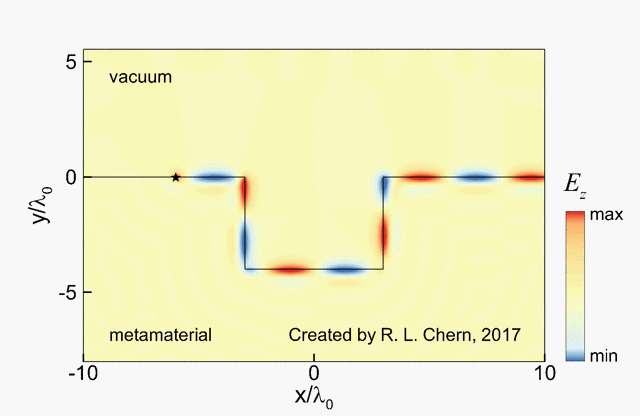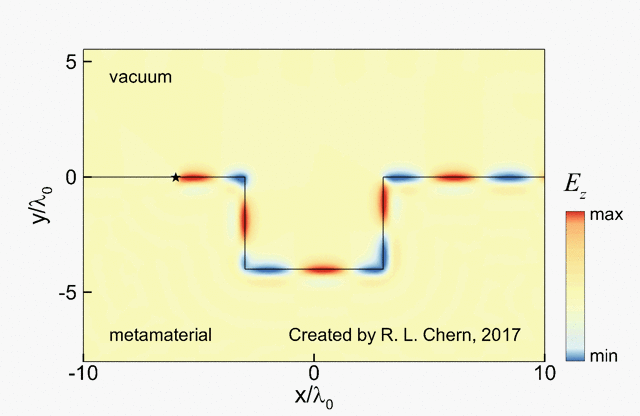
[1] R. L. Chern and Y. Z. Yu, "Chiral surface waves on hyperbolic-gyromagnetic metamaterials", Optics Express 25, 11801 (2017) [LINK]
[2] Y. Z. Yu and R. L. Chern, "Photonic topological phases in dispersive metamaterials", Scientific Reports 8, 17881 (2018) [LINK]
[3] J. R. Jiang, S. C. Wu, W. T. Chen and R. L. Chern, "Double Dirac cones in two-dimensional photonic crystals with C6 symmetry", Journal of Modern Optics 66, 2119-2130 (2019) [LINK]
[4] Y. Z. Yu, C. Y. Kuo, R. L. Chern, and C. T. Chan, "Photonic topological semimetals in bianisotropic metamaterials", Scientific Reports 9, 18312 (2019) [LINK]
[5] J. R. Jiang, W. T. Chen, and R. L. Chern, "Parity-time phase transition in photonic crystals with C6v symmetry", Scientific Reports 10, 15726 (2020) [LINK]
[6] R. L. Chern, Y. J. Shen, and Y. Z. Yu, "Photonic topological insulators in bianisotropic metamaterials", Optics Express 30, 9944 (2022) [LINK]
[7] R. L. Chern and Y. Z. Yu, "Photonic topological semimetals in bigyrotropic metamaterials", Optics Express 30, 25162 (2022) [LINK]
[8] R. L. Chern and Y. J. Chou, "Photonic Weyl semimetals in pseudochiral metamaterials", Scientific Reports 12, 18847 (2022) [LINK]
[9] R. L. Chern and Y. J. Chou, "Photonic topological phases in Tellegen metamaterials", Optics Express 30, 47004 (2022) [LINK]
[10] R. L. Chern, "Photonic helicoid-like surface states in chiral metamaterials", Scientific Reports 13, 13934 (2023) [LINK]
Bound States in the Continuum
Bound states in the continuum (BICs) are non-leaky localized resonance modes that coexist with a continuous spectrum of radiating waves1,2,3,4. Since BICs will not radiate to the far field, they are decoupled from the far-field radiation and possess infinite quality factors with zero spectral linewidths. In the presence of the absorption loss, roughness, or finite size of the structure, a theoretically true BIC is turned into a quasi-BIC with a finite quality factor.
[1] R. L. Chern, H. C. Yang, and J. C. Chang, "Bound states in the continuum in asymmetric dual-patch metasurfaces", Optics Express 31, 16570 (2023) [LINK]
[2] R. L. Chern, J. C. Chang, and H. C. Yang, "Bound states in the continuum in anisotropic photonic crystal slabs", Scientific Reports 13, 14139 (2023) [LINK]
[3] R. L. Chern and T. J. Hsu, "Bound states in the continuum in divided triangular hole metasurfaces", Scientific Reports 14, 13020 (2024) [LINK]
[4] R. L. Chern, S. W. Kao, and P. Y. Lin, "Multiple toroidal dipole bound states in the continuum in dielectric metasurfaces", Optics Express 33, 16863 (2025) [LINK]
[5] J. C. Chiang and R. L. Chern, "Evolution of topological polarization singularities in honeycomb photonic crystal slabs", Optics Express 33, 23782 (2025) [LINK]
Optics and Wave Computation
Numerical computational is an important approach to optics and wave problem. Our main focus is to employ or to improve computational methods for efficiently solving the physical quantities and investigating the underlying mechanism. Suitable physical models are also proposed for illustrating phenomena and designing functions.
Related publications:
[1] C. C. Chang, R. L. Chern, C. C. Chang, C. C. Chu, J. Y. Chi, J. C. Su, I. M. Chan, and J. F. Wang, "Monte Carlo Simulation of Optical Properties of Phosphor-Screened Ultraviolet Light in a White Light-Emitting Device", Japanese Journal of Applied Physics 44, 6056-6061 (2005) [LINK]
[2] Y. H. Liu, C. C. Chang, R. L. Chern, and C. C. Chang, "Phononic band gaps of elastic periodic structures: a homogenization theory study", Physical Review B 75, 054104 (2007) [LINK]
[3] C. Y. Kuo, R. L. Chern, and C. C. Chang, "Sound Scattering by a Compact Circular Pore", Journal of Sound and Vibration 319, 622-645 (2009) [LINK]
[4] R. L. Chern, C. Y. Kuo, H. W. Chen, and C. C. Chang, "Electromagnetic scattering by a subwavelength circular hole in a perfect metal plate of finite thickness: matched asymptotic expansion", Journal of the Optical Society of America B 27, 1031 (2010) [LINK]
[5] C. Y. Kuo, R. L. Chern, and C. C. Chang, "Multipole expansion of electromagnetic scattering wave by a small cylindrical pore on a perfect conducting semi-infinite half space", Progress In Electromagnetics Research B 26, 179-212 (2010) [LINK]
[6] R. L. Chern, H. E. Hsieh, T. M. Huang, W. W. Lin, and W. Wang, "Singular Value Decompositions for Single-Curl Operators in Three-Dimensional Maxwell's Equations for Complex Media", SIAM Journal on Matrix Analysis and Applications 36, 203-224 (2015) [LINK]
[7] T. M. Huang, T. Li, R. L. Chern, W. W. Lin, "Electromagnetic Field Behavior of 3D Maxwell's Equations for Chiral Media", Journal of Computational Physics 379, 118-131 (2019) [LINK]
Fluid Mechanics
Related publications:[1] C. C. Chang and R. L. Chern, "A numerical study of flow around an impulsively started circular cylinder by a deterministic vortex method", Journal of Fluid Mechanics 233, 243-263 (1991) [LINK]
[2] C. C. Chang and R. L. Chern, "Vortex shedding from an impulsively started rotating and translating circular cylinder", Journal of Fluid Mechanics 233, 265-298 (1991) [LINK]
[3] C. C. Chang, B. H. Liou, and R. L. Chern, "An analytical and numerical study of axisymmetric flow around spheroids", Journal of Fluid Mechanics 234, 219-246 (1992) [LINK]
[4] Y. J. Chou, C. J. Cheng, R. L. Chern, and C. Y. Hung, "Instabilities of particle-laden layers in the stably stratified environment", Physics of Fluids 31, 124101 (2019) [LINK]
[5] Y. J. Chang, R. L. Chern, and Y. J. Chou, "Transient instability in long, tilted water columns with fast-settling, particle-laden layers", Journal of Fluid Mechanics 929, A42 (2021) [LINK]
[6] Y. J. Chang, H. Y. Huang, R. L. Chern, and Y. J. Chou, "A multiscale computational framework using active learning to model complex suspension flows", Journal of Computational Physics 493, 12481 (2023) [LINK]
Teaching
Electromagnetism
This is a fundamental course of electromagnetic theory for students in the engineering school, which includes electrostatics, magnetostatics, and electrodynamics as three major topics. The electric fields in matter and magnetic fields in matter are also included as two related topics. A brief introduction of electromagnetic wave is included as a supplementary topic.
The goal of this course is to provide students with basic knowledge of electromagnetic theory, including physical concepts and mathematical skills for solving standard problems in electromagnetism.
Plot Gallery
This is a collection of plots used for illustrated examples in the course of electromagnetism.
The proposal should contain five parts: what, why, who, how, and where.
The what part is the description of the problem to be studied. The why part is the motivation for studying the problem. The who part is a review of literatures for related problems. The how part is the method to be used for studying the problem. The where part is the expected contributions to the problem. 1. Chinese is the formal language for the thesis, with auxiliary terms in English, if necessary.
1. The thesis contains three parts: title, abstract, and main text.
1. The abstract is a summary of your specific work.
1. The introduction contains at least three paragraphs.
1. Use MathType to create equations and variables in the thesis.
1. Each figure is referred at least once in the main text.
The codes for producing equations or figures are named by the equation or figure number in the thesis. 1. Each reference is referred at least once in the main text.
1. Prepare a paper.tex file (using template) and a paper.bib file (content from EndNote) that include the title (English), abstract (English), equations, figures, tables, and references.
1. Place thesis files in the the folder "thesis".
"Reading maketh a full man; conference a ready man; and writing an exact man."
"Write. Rewrite. When not writing or rewriting, read. I know of no shortcuts."
"Have a good and godly day, for of what lasting value is a good day if it's not also a godly day?"
There is no growth without change, no change without fear of loss, and no loss without pain.
A young man once asked God how long a million years was to him. God replied, "A million years to Me is just like a single second in your time." Then the young man asked God what a million dollars was to Him. God replied, "A million dollars to me is just like a single penny to you." Then the young man got his courage up and asked: "God, could I have one of your pennies?" God smiled and replied, "Certainly, just a second."
I never take medicine, unless you are medicine.
I'm not sure if I fall in love. If I do, I will be lonely.
Beauty is not only appearance on face but also attraction to mind.
The best reward to a good man is the fact of his being a good man.
Imperfection is more close to reality.
I miss you not because I am lonely. I am lonely because I miss you.
Loneliness is wild pleasure of one person. Wild pleasure is loneliness of a crowd of pepole.
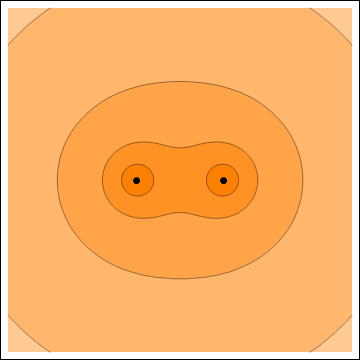

Electric potential (left) and electric field (right) of two point charges with the same sign
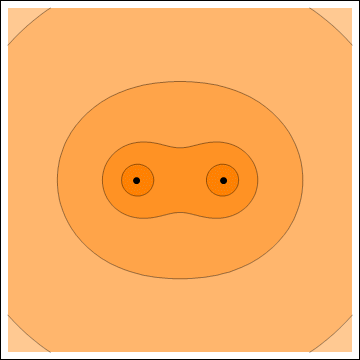

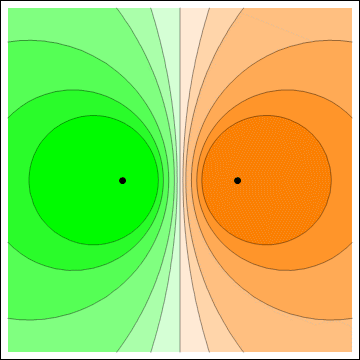
Electric potential (left) and electric field (right) of two point charges with opposite signs


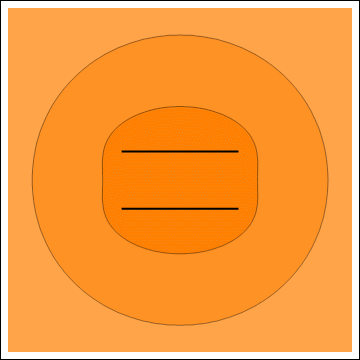
Electric potential (left) and electric field (right) for a line segment with change density of the same signs on two sides
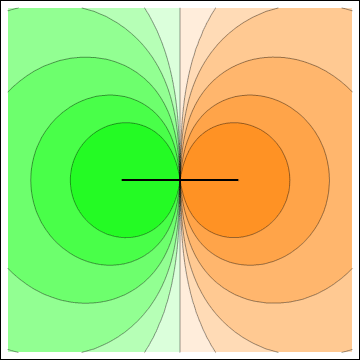

Electric potential (left) and electric field (right) for a line segment with change density of the opposite signs on two sides

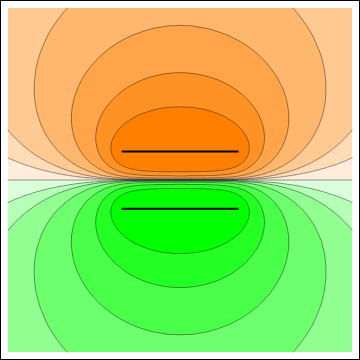
Electric potential (left) and electric field (right) for two parallel line segments with the same charge densities

Electric potential (left) and electric field (right) for two parallel line segments with opposite charge densities


Electric potential (left) and electric field (right) of a point charge outside a conducting sphere

Electric potential (left) and electric field (right) of two infinitely long wires, one with positive and the other with negative charge densities
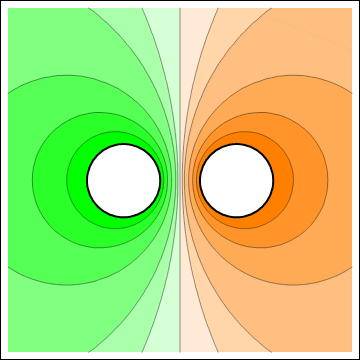
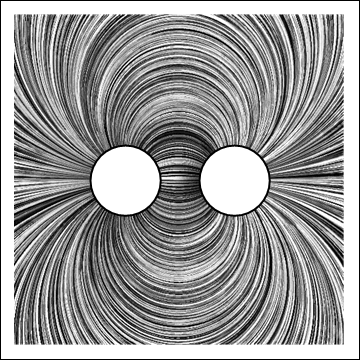
Electric potential (left) and electric field (right) of two conducting circular cylinders, one maintained at a positive potential and the other at a negative potential
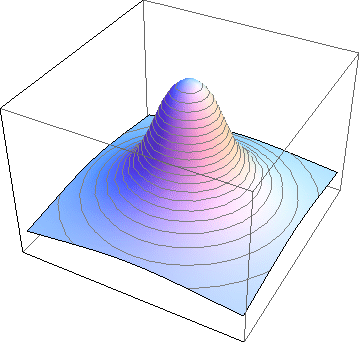
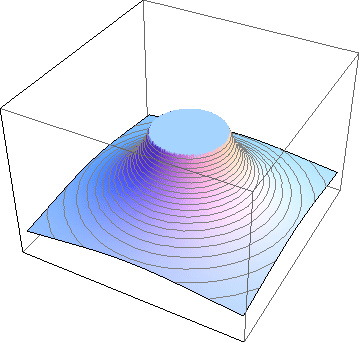
Electric potential of a uniformly charged solid sphere (left) or spherical shell (right)
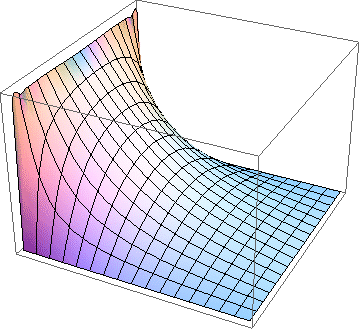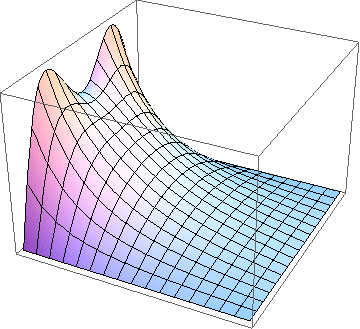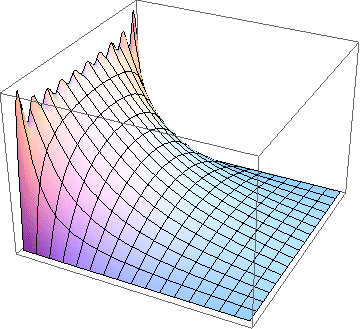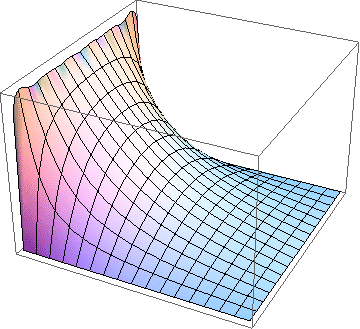
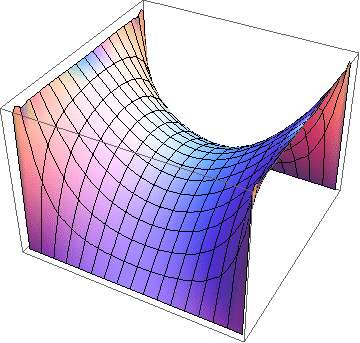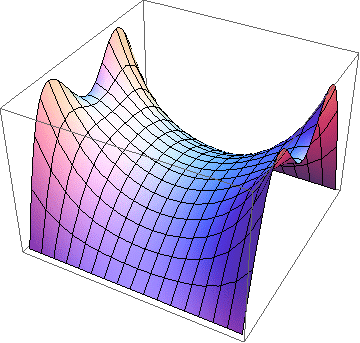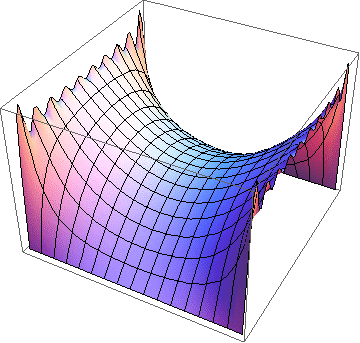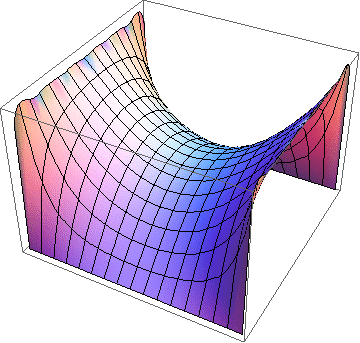
Electric potential inside a conducting square pipe with one side (left) or two sides (right) maintained at a constant potential and the other sides grounded
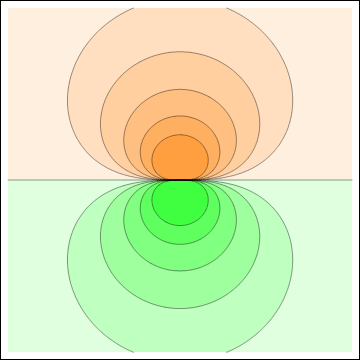

Electric potential (left) and electric field (right) of a pure dipole
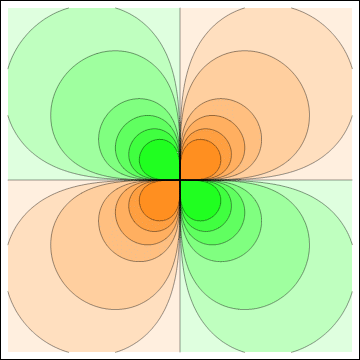

Electric potential (left) and electric field (right) of a pure quadrupole
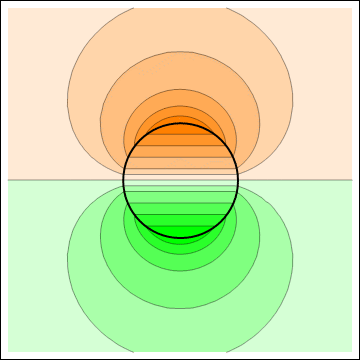

Electric potential (left) and electric field (right) of a uniformly polarized sphere
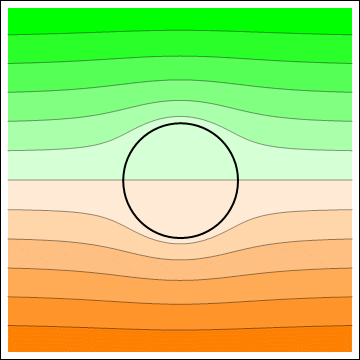

Electric potential (left) and electric field (right) for a dielectric sphere placed in an otherwise uniform electric field


Magnetic field for two infinitely long straight line currents with the same (left) and opposite (right) directions


Magnetic field for an infinitely long thin strip with the same (left) and opposite (right) directions on two sides


Magnetic field for two parallel infinitely long thin strips with the same (left) and opposite (right) directions
Guidelines for preparing a thesis
Content:
What:
Why:
Who:
How:
Where:
Guidelines for writing a thesis
Language:
2. Use English sentence patterns to write Chinese sentences in the thesis.Content:
2. The main text contains four sections: introduction, theory, results and discussion, and conclusion.
3. An English abstract is also needed.Abstract:
2. Do not include general descriptions of the problem in the abstract.Introduction:
2. The first paragraph is a review of previous research related to the thesis.
3. The second paragraph is the significance (both in theory and application) of the research, and the connection to your present work.
4. The third paragraph is the description of your work.Equations:
2. Do not use keyboard to input parentheses, brackets, and braces in the equations.
3. The variables and constants in the equation are defined or explained in the main text.
4. Equations are automatically numbered in the thesis.
5. Place bracket outside the parenthesis and brace outside the bracket.
6. Use bold face characters to denote vectors.
7. Place a hat "^" over the coordinate axis name to denote unit vector.
8. Underline the characters to denote matrices.
9. Use subscript or superscript to denote components.
10. Use parenthesis for vectors in component form.
11. Use bracket for matrices in entry form.
12. Equations are parts of the sentence in the text. A punctuation after the equation might be necessary.Figures:
2. All figure files are created by plotting softwares rather than copying from the screen.
3. All figures in the thesis are the same as generated by codes or softwares, without further modifications by other means.
4. Do not use Microsoft Office to create and modify the figures.
5. The size of labels and numbers in the figure is not less than 80% of the character size in the main text.
6. If a figure contains multiple plots, add the label (a), (b),... to the top left corner of each plot in the text rather in the plots.
7. All parameters used in the figure are declared in the figure caption.
8. A colorbar is needed for shading contours.
9. Contour labels are needed for non-shading contours.
10. Figures are automatically numbered in the thesis.Codes:
References:
2. The information of all references in the thesis is included in an EndNote file.
3. Use the abbreviated journal title in ISI Web of Knowledge to edit the journal name in the EndNote file.
4. The pdf file of each paper can be opened from the EndNote file.
5. All references in the thesis are inserted from the EndNote file. (How to do it?)Latex documents:
2. Minimal text (English) for identifying the references, the variables in equations, and the captions in figures are required.
3. Using eps format for figure files.
4. Using author's last name, followed by last two digits of the year, for citing the reference, e.g. "\cite{chern14}".
5. Using MikTeX to generate paper.pdf from paper.tex and paper.bib.
File folders:
2. Place figure files in the folder "figure".
3. Place codes in the folder "code".
4. Place latex files in the folder "latex".
4. Place EndNote file in the folder "endnote".
5. Place reference files in the folder "reference".
6. The filename of the reference is the same as the title of the reference (Capitalize the first letter only, except for proper/actual item names).
Pondering
Francis Bacon (1561-1626)
Larry L. King (1929-2012)
Woodrow Kroll (1944-)
Rick Warren (1954-)
Bits and Pieces
French Blue
French Blue
French Blue
French Blue
French Blue
French Blue
French Blue